And now, what's going to happen to us without barbarians?
They were, those people, a kind of solution.
[C. Cavafy, "Waiting for the Barbarians"]

The Surface Patch Library (SPL) includes a set of curved surface patch models to geometrically represent areas on and around the robot. A local mapping and tracking system assembles patches in the environment and on the robot into a spatial map to be used when a robot operates (e.g., for locomotion or manipulation) in the environment.



The current version of the SPL sourcecode is now available as a Matlab toolbox: https://github.com/RoViL-Team/spl
[The SPL C++ library is coming soon as a ROS node.]


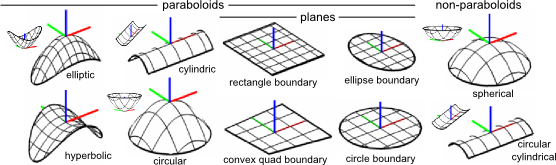
The 10 bounded curved-surface patch types are designed to model local contact regions both in the environment (e.g. on rocky surfaces) and on a robot (e.g. foot pads). The system uses minimal geometric parameterizations based on the exponential map for spatial pose, both in the usual 6DoF case and also for patches with revolute symmetry that have only 5DoF. A fitting algorithm is included to fit and perceptually validate any patch type to point samples of a surface, with quantified uncertainty throughout using covariance matrices, both in the input points (including nonuniform variance, common in data from range sensors) and in the output patch. Moreover, we apply simultaneous localization and mapping (SLAM) techniques to assemble patches on-line into a spatial patch map of the available contact surfaces both on and around a robot. We test the algorithms in a real-time foothold perception system where a mini-biped robot (RBPB), a half-size (COMAN), and a full-size (WALK-MAN) humanoid robot perform foot placements and locomotion on regular and irregular (e.g. rocks) terrain types, reasoning about contacts.


The WALK-MAN full-size humanoid robot stepping on flat and curved surfaces in a 5-step locomotion process after a contact analysis based on patches.



The COMAN half-size humanoid robot stepping on flat and curved surfaces after a contact analysis based on patches.



Overview of the total patch mapping and tracking system, which splits in two parts: perception (left) and motion control (right).
The RPBP small-size biped is stepping on curved surfaces using the patch map and a set of predefined predefined step motions.

Research References

Some of the mathematical foundations of the system are described in the following works:
  1. "Visual Grasp Affordance Localization in Point Clouds using Curved Contact Patches", Dimitrios Kanoulas, Jinoh Lee, Darwin G. Caldwell, and Nikos G. Tsagarakis (IJHR'16) [.pdf]
  2. "WALK-MAN: A High Performance Humanoid Platform for Realistic Environments", N. G. Tsagarakis et. al. (JFR'16)
  3. "Uncertainty Analysis for Curved Surface Contact Patches", Dimitrios Kanoulas, Nikos G. Tsagarakis and Marsette Vona (Humanoids'16) [.pdf]
  4. "Rough Terrain Perception for Bipedal Robots using Curved Contact Patches", Dimitrios Kanoulas (IROS'15 Workshop) [.pdf]
  5. "Curved Surface Patches for Rough Terrain Perception", Dimitrios Kanoulas (Ph.D. Thesis) [.pdf]
  6. "Bio-Inspired Rough Terrain Contact Patch Perception", Dimitrios Kanoulas, Marsette Vona. (ICRA'14) [.pdf]
  7. "The Surface Patch Library (SPL)", Dimitrios Kanoulas, Marsette Vona. (ICRA'14 Workshop) [.pdf]
  8. "Sparse Surface Modeling with Curved Patches", Dimitrios Kanoulas, Marsette Vona. (ICRA'13) [.pdf]
  9. "Surface Patches for Rough Terrain Perception", Dimitrios Kanoulas (NERC 2013) [.pdf]
  10. "Curved Surface Contact Patches with Quantified Uncertainty", Marsette Vona, Dimitrios Kanoulas (IROS'11) [.pdf]

Videos

Kinect Rock Data with Manual Segmentation ogv|mp4|webm

This demo shows interactive segmentation of patches from real data taken with a Kinect, with each patch automatically fit by our patchfit algorithm. To reproduce, run testrock.

Fit Elliptic Paraboloid (Simulation) ogv|mp4|webm

This demo starts with a simulated “ground truth” elliptic paraboloid patch. Data samples are then taken with noise simulated according to our Kinect range error model. Finally, a paraboloid patch will ellipse boundary is automatically fit with our patchfit algorithm. To reproduce, run testpatchfit(1,‘dbg’,3).

Fit all Patch Types (Simulation) ogv|mp4|webm

Similar to the elliptic paraboloid demo, but shows the results when run on “ground truth” instances of all 10 patch types. To reproduce, run testpatchfit(1:10,‘dbg’,6).



Open-Loop Locomotion for Patch Mapping and Tracking on a Biped Robot (RBPB)



Foot Placement using Patch Mapping and Tracking on a Biped Robot (RBPB)



Foot Placement and Locomotion using Patch Contact Analysis on a Half-Size (COMAN) and a Full-Size (WALK-MAN) Humanoid Robot